向 量 處 理 規 則
向量表示法、向量和、向量差

向量即為有方向之物理量，如位移、速度、加速度、力、動量、電力、磁力、重力場、電場、磁場、、、、等。

處理此等物理量之四則運算時，有其特殊規則，需考慮方向，不是直接以數字處理即可。

向量繪圖：向量是有方向之物理量，一般繪成 ，
＊＊ 箭頭長度代表向量大小，箭頭方向為向量方向。
＊＊ 向量長度比例是否正確，對處理結果有舉足輕重的影響，不是隨意畫出一段任意長度即可。

向量平移：在做向量處理時，我們時常需要把不同地點之向量畫在一起，此時需把向量作 不改變原向量大小、方向的平行移動。

一、向量之加法：

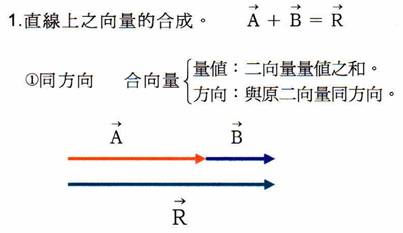
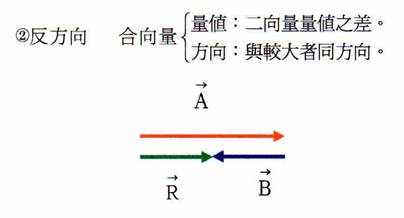
若需合成之二向量其方向間夾一角度，則需先把向量平移。
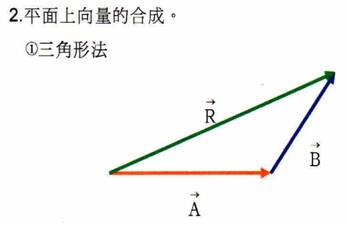
三角形法：二向量箭頭串接，其和向量由第一個向量的箭尾，畫至第二個向量的箭尾。
                  若有數個向量相加，則把所有向量串接起來即可得和向量。
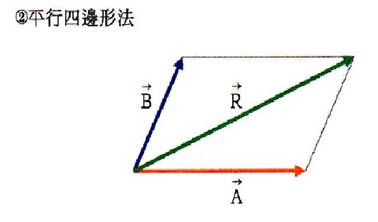
平行四邊形法：如圖，注意A、B、R向量之箭頭方向。

如下圖，一人由左下方出發，走了六段，其總位移之大小、方向由圖即可繪出。

向量合成之大小、方向：若A、B向量彼此垂直，以畢氏定理求之即可。
                         但若A、B向量彼此非平行或垂直，則需以圖形、
                                數學之三角函數法共同處理才可以。

二、向量之減法：
在繪圖上可以想成  ，由B箭頭（藍色）處畫一向量朝著A箭頭（紅色）處，即為C向量（圖上之黃色箭頭）。

三、向量和、差之應用：

1.      求位移：A至B點之位移，即為  
（位置向量：由參考點，即座標原點，畫一個箭頭指向A位置，即為A點位置向量）

2.     求速度變化、加速度：
所有運動不一定是一直線，若運動方向改變，其速度變化、加速度，需以向量規則處理。

3.     求合力：若是一個物體上，同時有數力作用，該物受力後之運動，需把這數力向量相加。

四、向量分解及其應用：(Link)

向量除了和差問題外，還有分解的概念，乘除的問題，在物理上用途極大，另闢章節討論之。

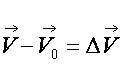問題：

等速率圓週運動的加速度方向向哪裡？