向 量 的 分 解

以下四個例題，適當的說明了向量分解之原因、方法，分解後彼此垂直之分量具獨立性，
各分量對運動之影響，請仔細觀察、思考。

例一、斜向上施力拉一個皮箱，使皮箱前進的力多大？

例二、斜向上拋一物體，物體往前的速度，往上的速度各如何？

例三、小孩子坐在一光滑溜滑梯上，使小孩往下滑的力多大？小孩往下滑的加速度多大？

例四、拋體運動之切線與法線加速度。

以上三個例子中，力、速度、加速度都是向量，在處理上有其規則。

〈例一說明〉
斜向上的力F可分解成水平F_x、鉛直F_y兩個分力。（注意：一定要畫成矩形）
F_x＝F cosθ（綠色箭頭）
F_y＝F sinθ（紅色箭頭）
使物體往前加速的力量大小是F_x＝F cosθ
使物體與地面間正向力減少的是F_y＝F sinθ

〈例二說明〉
斜向上拋一物體，其速度分量圖如同例一。
球離手後，以  水平速度 V_x＝V cosθ向前，鉛直初速V_y＝V sinθ 向上

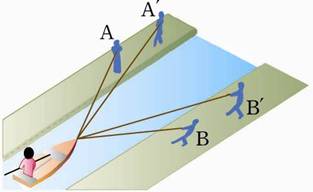
〈圖片說明〉
四個人共同拉一艘船，如何用力，船才會乖乖的走在河道中央？原理？
右上圖中，使車往前的力多大？產生多大加速度？

〈例三說明〉
如右圖，質量 m 放在傾斜角為 θ 之斜面上
物體受重力mg（藍色箭頭），此力可分解成
平行斜面分力（往下滑）F_t＝mg sinθ（綠色箭頭）
垂直斜面分力（正向力）F_x＝mg cosθ（紅色箭頭）
★☆☆★所以，
一個由斜面自由滑下之物體做等加速度運動，
其加速度大小a＝g sinθ

〈範例練習〉如附圖，一物在仰角37°之光滑斜面底端，以v₀初速沿斜面向上滑行，歷時8秒滑回原出發點，則其在斜面之最大位移為______m。（g＝10 m/s²）   

詳解： 1. 由仰角37°之光滑斜面，可知 a＝g sinθ＝6 m/s²
      2. 歷時8秒滑回原出發點,可知往上時間（或往下時間）為4秒
      3. 由等加公式可得答案。 答案：48

〈例四說明〉
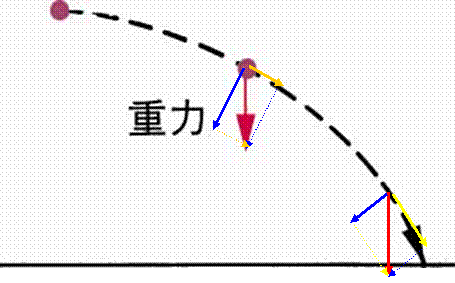
一個物體往外拋，在球離手後，物體只受重力（鉛垂方向）作用，而有一向下之加速度，至於物體的軌跡則因出發時之速度方向、大小而不同。

在運動的過程中，重力加速度（紅色箭頭）可分解為兩個方向的分量
切線加速度：與運動方向（速度方向）平行之加速度（黃色箭頭）──為物體速度大小改變之原因。
法線加速度：與運動方向（速度方向）垂直之加速度（藍色箭頭）──為物體速度方向改變之原因。