平 均 速 度

以上三個圖形表示直線運動時，位置─時間的關係圖。

圖一：靜止。    圖二：速度為正。    圖三：速度為負。

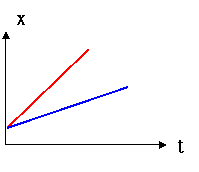
平均速度之求法： 右圖表示非等速度運動之圖形，如何求該運動中任何時段之平均速度、及任何時刻之瞬時速度 1. 以定義求之。(數字、符號處理) 2. 以x-t圖求割線斜率。   如右圖，以AB直線為直角三角形斜邊，   底邊為 ，高為   則 平均速度為v-t 圖割線斜率。

瞬時速度

瞬時速度：    lim是limit之縮寫，是指極小值之意。
其中 表示 t₂非常接近t₁ ，也可寫成，都是指極短暫的時間。
如圖，t₁ 時刻之瞬時速度為切過該點之切線斜率。

例如：12點到12點又0.1秒之間的平均速度，視同12點時之瞬時速度。

瞬時速度之求法：

1.    瞬時速度為v-t 圖切線斜率。
實際上不可能畫出x-t 圖，再據以求切線斜率，微分就是求斜率的數學方法。

2.    以定義求之。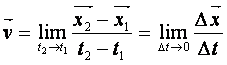    How  to  do？
   例如：  （此式子表示，x是t的函數）
在時刻t時之瞬時速度 ：                     
                       

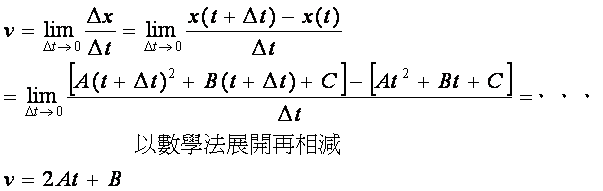
3.     以微分公式處理：
   例如：
        
    其中表示對時間微分的意思，微分規則是

                   指數乘係數，指數降一位，常數項微分＝0。
 例如：