![]()
![]()
![]() 隨著時間的增加
隨著時間的增加
![]()
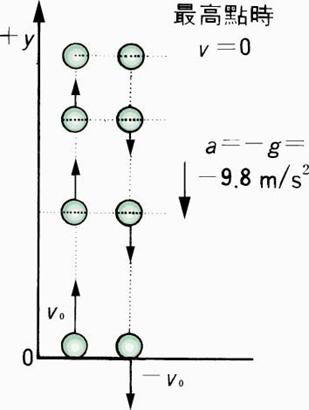
還在往上過程
![]()
在出發點上方
![]()
到達最高點
![]()
回到出發點
![]()
物體正在往下
![]()
在出發點下方
直線運動之拋體運動
一、 方向與符號問題:
〈例一〉一石由頂樓向上鉛直拋出,其拋出速度為40(m/s)。已知頂樓的高度為100(m),則該石子經過多久落地(g=10m/s2)? (A)2 (B)4 (C)8 (D)10 (s)。 D
1.
自由落體與下拋:
初速、加速度、末速、位移
方向都相同,應沒有符號問題,一般以向下為正。
2.
上拋問題:
初速向上(為正)、加速度向下(為負)。
|
|
|||
|
|
還在往上過程 |
|
在出發點上方 |
|
|
到達最高點 |
|
回到出發點 |
|
|
物體正在往下 |
|
在出發點下方 |
二、 時間的問題:
〈例二〉某物作自由落體運動,若不考慮空氣阻力,則第3秒內的位移與3秒內的位移量值之比為何? (A) 1:1 (B) 5:9 (C) 1:3 (D) 1:5 (E) 1:5。 B
〈例三〉某物作自由落體,已知其落地費時4秒,則落體前一秒落下的距離,是全程的______。
答案:![]()
自由落體之物體:
![]()
1. 由出發點開始計量:
|
時距 |
1秒內 |
2秒內 |
3秒內 |
4秒內 |
5秒內 |
6秒內 |
7秒內 |
、、、、、 |
|
位移比例 |
1 |
4 |
9 |
16 |
25 |
36 |
49 |
、、、、、 |
2. 第﹍﹍﹍秒之計量
|
時距 |
第1秒 |
第2秒 |
第3秒 |
第4秒 |
第5秒 |
第6秒 |
第7秒 |
、、、、、 |
|
位移比例 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
、、、、、 |
解釋:畫一時間軸數線,五秒內是指0-5秒內之時距。而第五秒是指4-5之間的時距。
3.
落地前一秒落下的距離:假設落地需時t秒
方法一:畫V-t
圖,自由落體為通過原點的斜直線,t秒內位移為0-t秒之曲線下三角形面積,落地前一秒落下的距離為時間
![]() 之梯形面積。
之梯形面積。
計算上以t秒內之三角形減去
![]() 秒內之三角形較為簡易。
秒內之三角形較為簡易。
方法二: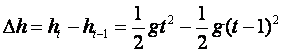
三、 上拋運動之對稱性
〈例三〉一籃球自地面鉛直上拋,當其通過離地面15 m高之旗竿頂時,兩次之時間間隔為2秒,則此籃球上拋之初速度為______m/s。(g=10 m/s2)答案:20
|
高度與時間 |
1. |
由
|
|
2. |
上升總時間與下降總時間相同。 |
|
|
高度與速度 |
1. |
由
|
|
2. |
上升過程與下降過程完全對稱。 |
1.
上升過程與下降過程是完全對稱的
![]()
![]()
![]()
2.
所以上面〈例三〉中,籃球自最高點落至旗竿頂,需時1秒。此題可以由籃球自最高點開始以自由落體計算高度、末速等。
其落地之末速大小等於拋出時之初速。