張力概念、問題解析

 〈概念〉施力於物體，會使物體改變運動狀態或變形。力是物體間的交互作用，因此有關力的問題，時常要考慮到所談的力，究竟是作用於哪一物體。

 〈解題方法〉張力問題，基本上就是F=ma的問題，所以在解題時可依照下列步驟循序分析

  例題一：
以上圖為例，如何求m₁、m₂、m₃系統之加速度及m₁、m₂間繩子張力與m₂、m₃間繩子張力。

  〈步驟一〉先選好目標，即受力之對象，也就是你的系統。
在此，共有六種可能，【m₁、m₂、m₃】，【m₁、m₂】，【m₂、m₃】，【m₁】，【m₂】，【m₃】。

  〈步驟二〉畫出你的系統的受力圖，在畫圖之前因為不知道繩子之張力，故假設為T₁，T₂

說明：
1. 對所有未知數，自訂代號，列出方程式。如本題之T₁，T₂， a。
2. 本題之未知數有三個，雖然上面列出了六個，實際上只要三個方程式即可求解。
3. 習慣上，先以第六式求得加速度後，再代入其它式子求張力。
4. 系統內之力（稱為內力，如【m₁、m₂、m₃】為系統時之T₁，T₂），
    並不影響系統之加速度，所以不予考慮。
5. 系統受力，只要考慮系統所受外力即可。

例題二：
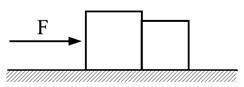
二物體質量之比為3：2，今將二者緊靠置於平滑桌面上，施水平力(F)於質量大者，使其水平滑動，則此二物間相互作用之力為　　　F。

分析：
1. 此題與例題一乍看之下不同，其實相同。二物體之間之正向力，相當於上題中之繩子張力。
2. 假設二物體間互相作用之正向力大小為N。左物m₁，右物m₂。
3. 畫出左物m₁，右物m₂之力圖。
4. F=ma 列出方程式，求解。
  
  
  

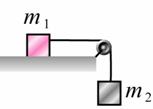
例題三：
 

分析：
1. 假設繩子張力T，系統加速度a。
2. 畫出m₁力圖、m₂力圖、m₁、m₂合系統力圖。
3. 列出方程式，求解。